Os números primos são fundamentais para a criptografia moderna. Algoritmos assimétricos dependem inteiramente de encontrar dois números primos gigantes (maiores de 200 casas decimais) que multiplicados resulte em um número ainda maior! Por exemplo, o último número “N” fatorado da RSA foi o RSA-250 que continha 250 casas. O número era 2140324650240744961264423072839333563008614715144755017797754920881418023447140136643345519095804679610992851872470914587687396261921557363047454770520805119056493106687691590019759405693457452230589325976697471681738069364894699871578494975937497937. Este número era o resultado da multiplicação de dois números:
64135289477071580278790190170577389084825014742943447208116859632024532344630238623598752668347708737661925585694639798853367
e
33372027594978156556226010605355114227940760344767554666784520987023841729210037080257448673296881877565718986258036932062711
Esses dois números são os primos que tornavam a RSA-250 possível (leia este post se estiver com dúvidas).
Um método bastante simples e eficiente para encontrar números primos é o “Crivo de Eratóstenes”. Os passos são estes:
- Colocamos todos os números de 2 até um limite qualquer.
- Encontramos a raiz quadrada do número limite
- Cortamos todos os múltiplos de primeiro primo, ou seja, 2
- Cortamos todos os múltiplos do próximo número que sobrou, ou seja, 3
- Cortamos todos os múltiplos do próximo número que sobrou, ou seja, 5
- Continuamos cortando até os múltiplos do número limite que encontramos no passo 2
- Todos os números que sobraram são primos!
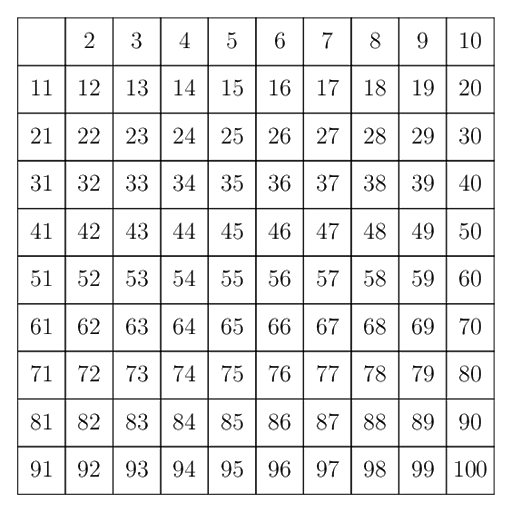
Nessa imagem coloquei todos os números de 2 até 100.
Neste caso vou buscar até 100. A raiz quadra de 100 é 10. Se desse uma dízima periódica, usaríamos apenas a parte inteira. Ou seja, se quiséssemos buscar todos os primos até 200, usaríamos como resultado “14”.


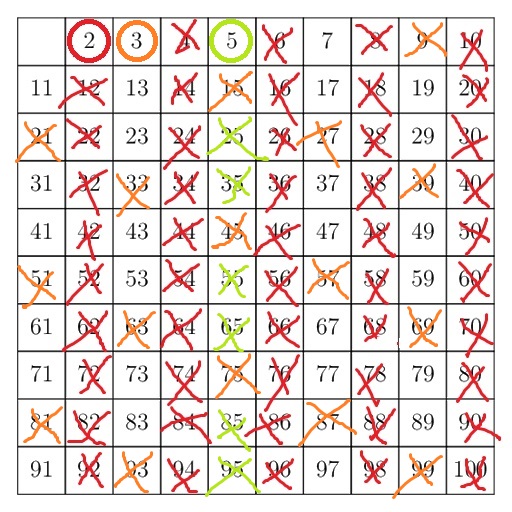
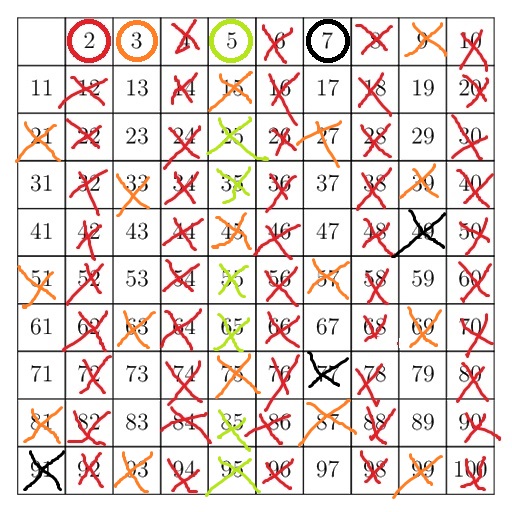
Neste caso cortaríamos todos os múltiplos de 2 até 10. Mas só precisamos ir até 7 porque depois dele não haviam sobrado números menores ou iguais a 10.
Portanto, neste exemplo, os primos de 2 a 100 são: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89 e 97
Abaixo uma pequena animação mostrando estes passos. Veja que o autor procura os primos de 2 a 120. A raiz quadrada de 120, considerando apenas a parte inteira, é 10. Então assim como neste artigo, ele só corta os múltiplos até 10 (na prática até 7, já que múltiplos de 8 são múltiplos de 2 também, múltiplos de 9 são múltiplos de 3 também e múltiplos de 10 são múltiplos de 2 também).
